Formal verification (FV) has witnessed growing significance with current emerging program synthesis by the evolving large language models (LLMs). However, current formal verification mainly resorts to symbolic verifiers or hand-craft rules, resulting in limitations for extensive and flexible verification. On the other hand, formal languages for automated theorem proving, such as Isabelle, as another line of rigorous verification, are maintained with comprehensive rules and theorems. In this project, we propose FVEL, an interactive Formal Verification Environment with LLMs. Specifically, FVEL transforms a given code to be verified into Isabelle, and then conducts verification via neural automated theorem proving with an LLM. The joined paradigm leverages the rigorous yet abundant formulated and organized rules in Isabelle and is also convenient for introducing and adjusting cutting-edge LLMs. To achieve this goal, we extract a large-scale FVELer. The FVELer dataset includes code dependencies and verification processes that are formulated in Isabelle, containing 758 theories, 29,125 lemmas, and 200,646 proof steps in total with in-depth dependencies. We benchmark FVELer in the FVEL environment by first fine-tuning LLMs with FVELer and then evaluating them on Code2Inv and SV-COMP. The results show that FVEL with FVELer fine-tuned Llama3-8B solves 17.39% (69→81) more problems, and Mistral-7B 12% (75→84) more problems in SV-COMP. And the proportion of proof errors is reduced..
 FVEL Environment
FVEL Environment

FVEL workflow.
The main idea of the  FVEL environment is to provide an interactive environment with large language models (LLMs) that leverage rigorous theorem-proving processes. The input of
FVEL environment is to provide an interactive environment with large language models (LLMs) that leverage rigorous theorem-proving processes. The input of  FVEL environment is a code to be verified. Specifically, we currently verify C code and conduct a pilot study on our new framework. Moreover, the input format is flexible as one can choose to input an ensemble of C code and its corresponding SIMPL and/or Isabelle content as supplements. The output of
FVEL environment is a code to be verified. Specifically, we currently verify C code and conduct a pilot study on our new framework. Moreover, the input format is flexible as one can choose to input an ensemble of C code and its corresponding SIMPL and/or Isabelle content as supplements. The output of  FVEL is the code verification result.
FVEL is the code verification result.
 FVEL interacts with a large language model to achieve the verification. At the initial step of interaction (S0),
FVEL interacts with a large language model to achieve the verification. At the initial step of interaction (S0),  FVEL transforms the input C code into facts, and then provides the facts to the LLM. The LLM then generates a lemma in Isabelle as a formal description of the code specification. In this step, a code verification problem is transformed into an ATP problem. As a result,
FVEL transforms the input C code into facts, and then provides the facts to the LLM. The LLM then generates a lemma in Isabelle as a formal description of the code specification. In this step, a code verification problem is transformed into an ATP problem. As a result,  FVEL can leverage the LLMs theorem-proving techniques and rigorous ATP validation. At the follow-up interaction steps (Si, i ≥ 1), the LLM is prompted to generate proof steps, while
FVEL can leverage the LLMs theorem-proving techniques and rigorous ATP validation. At the follow-up interaction steps (Si, i ≥ 1), the LLM is prompted to generate proof steps, while  FVEL incorporates an Isabell prover to provide feedback such as error messages to the LLM. The process terminates until a whole proof is generated. If the proof success in proving the lemma,
FVEL incorporates an Isabell prover to provide feedback such as error messages to the LLM. The process terminates until a whole proof is generated. If the proof success in proving the lemma,  FVEL outputs "success", otherwise outputs "failure".
FVEL outputs "success", otherwise outputs "failure".
 FVELer Dataset
FVELer Dataset
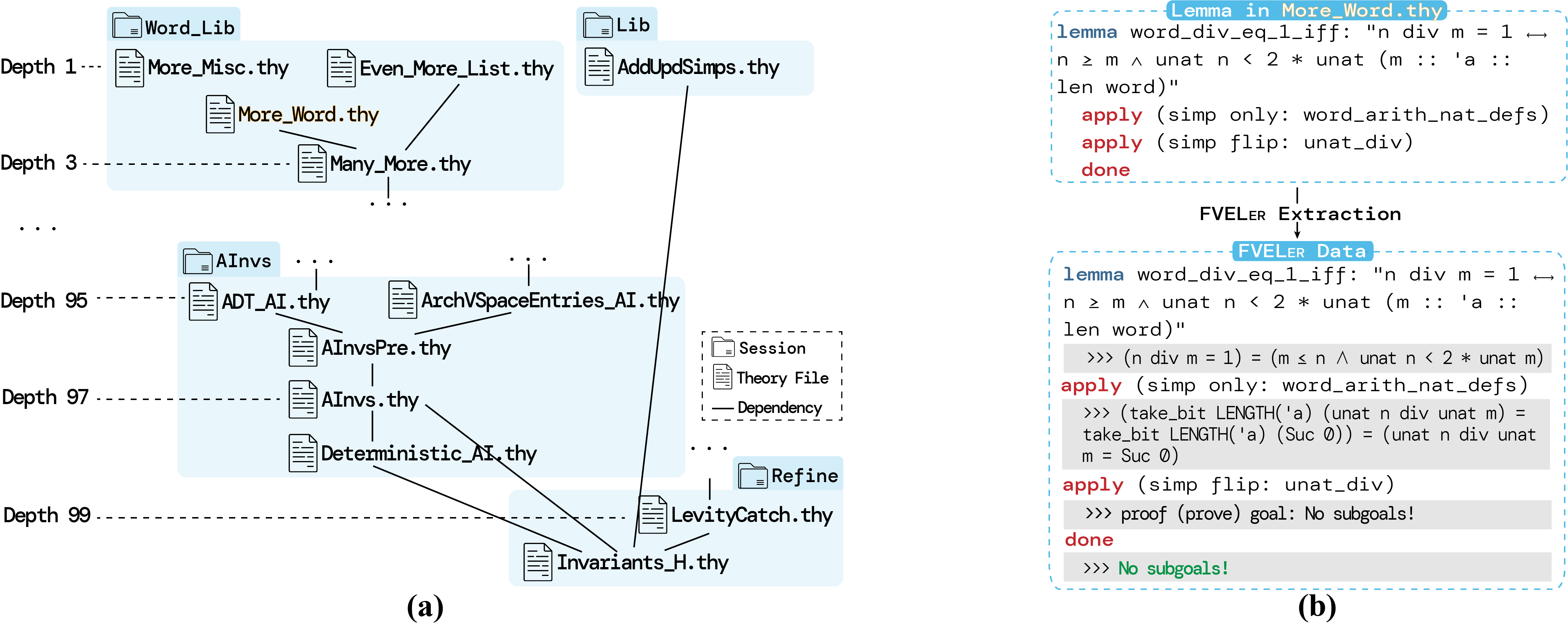
FVELer construction.
 FVELer contains transformed Isabelle theories and lemmas from C codes that support the FVEL environment for C code verification. It has two main components:
FVELer contains transformed Isabelle theories and lemmas from C codes that support the FVEL environment for C code verification. It has two main components:
You can download the dataset on GitHub.
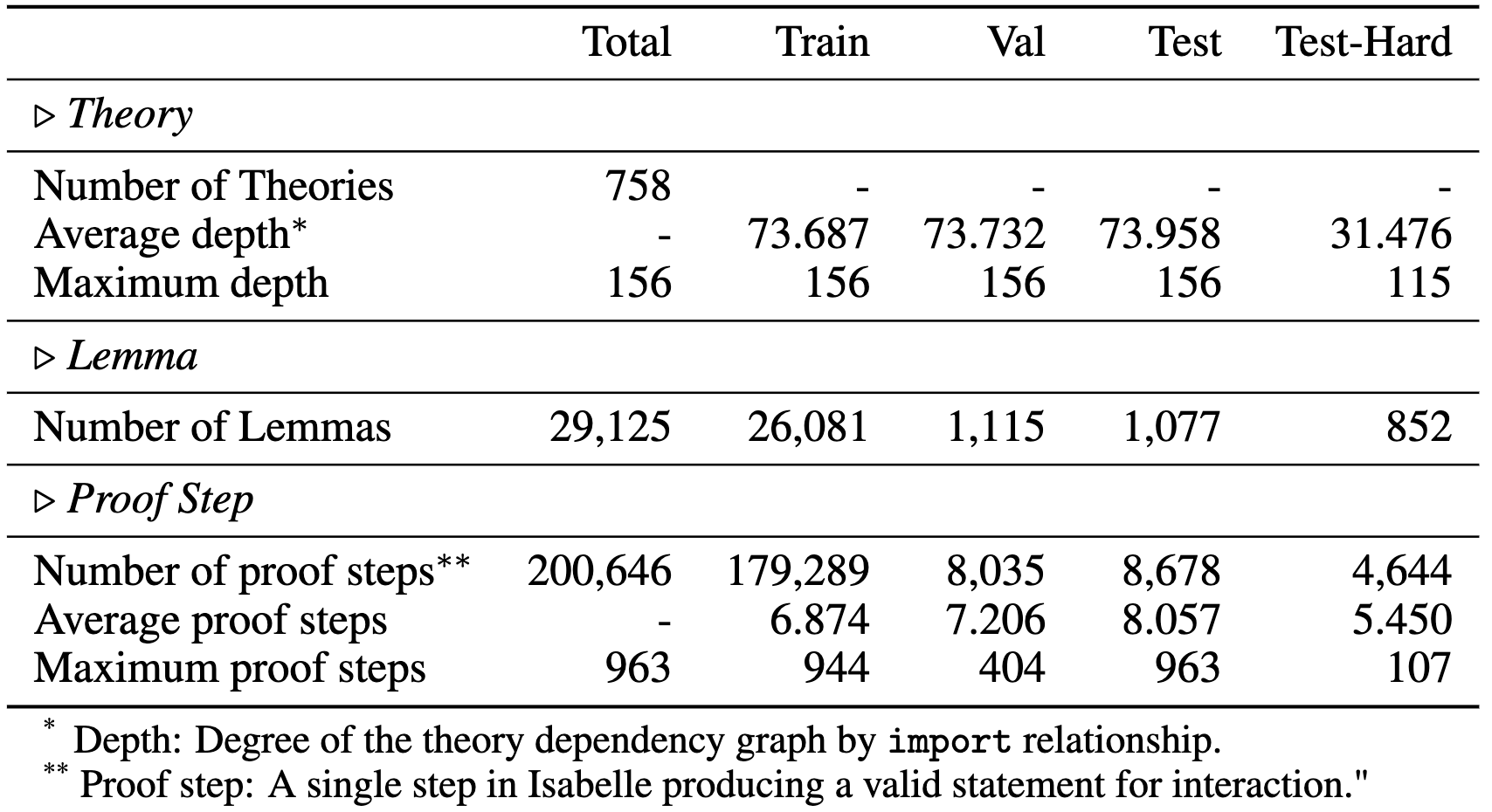
The statistics of  FVELer dataset.
FVELer dataset.
 FVELer contains contains 758 theories, 29,125 lemmas, and 200,646 proof steps in total with in-depth dependencies. We randomly split FVELer according to lemmas, resulting in a training set, a validation set, a test set, and an especially selected test-hard set. The test-hard set is selected from those lemmas in the three sessions SysInit, SysInitExamples, LibTest. Such lemmas are in higher depths in the dependency relationship, therefore they have less import relationships by other theories.
FVELer contains contains 758 theories, 29,125 lemmas, and 200,646 proof steps in total with in-depth dependencies. We randomly split FVELer according to lemmas, resulting in a training set, a validation set, a test set, and an especially selected test-hard set. The test-hard set is selected from those lemmas in the three sessions SysInit, SysInitExamples, LibTest. Such lemmas are in higher depths in the dependency relationship, therefore they have less import relationships by other theories.
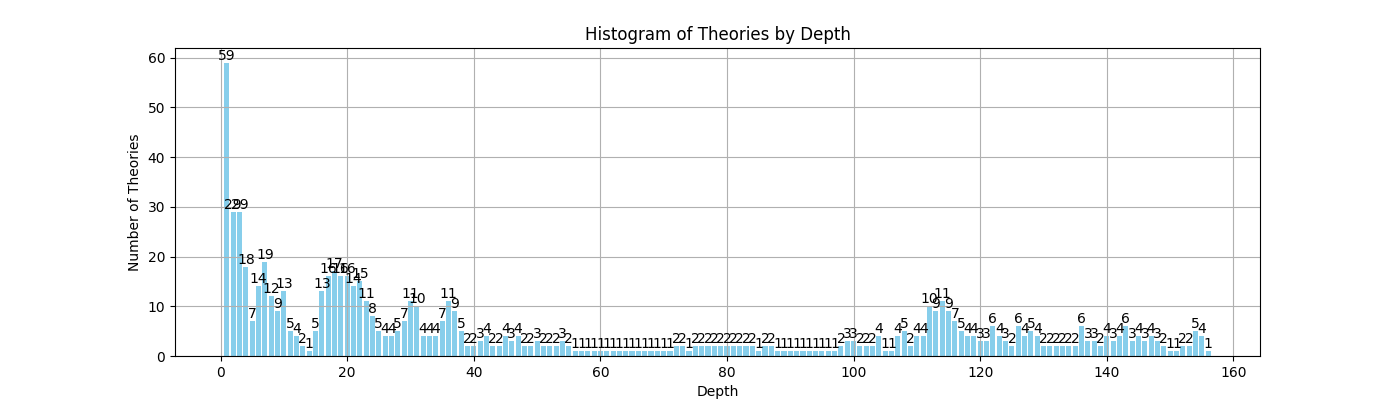
Distribution of dependency by theory

Distribution of dependency by lemma.

The FVELer lemma distribution over step intervals.

sel4_extraction/ folder example.

dataset_lemma_split.json example.

sel4_thy_info.json example.

sel4_session_info.json example.
Given a formal verificaiton case that is converted to an Isabelle lemma as the input, The upper row shows a case in which FVEL-Mistral-7B correctly applies the lemma learned from fine-tuning, thus correcting and simplifying the proof. Contrastively, Mistral-7B generates common not_eq_complement without considering a reasonable proof strategy, resulting in a failed proof. In the second case, Mistral-7B rewrites the lemma statement into “assumes” and “shows” statements, according to which gives an incorrect proof. FVEL-Mistral-7B, on the other hand, expands the brackets in the equation and then is able to derive contradiction according to “(bAND NOT b)”, and completes the proof via the contradiction of the right-hand side of the equation.

Generated proofs by Mistral-7B and FVEL-Mistral-7B.
@inproceedings{lin2024fvel,
title={{FVEL}: Interactive Formal Verification Environment with Large Language Models via Theorem Proving},
author={Xiaohan Lin* and Qingxing Cao* and Yinya Huang* and Haiming Wang* and Jianqiao Lu and Zhengying Liu and Linqi Song and Xiaodan Liang},
booktitle={The Thirty-eight Conference on Neural Information Processing Systems Datasets and Benchmarks Track},
year={2024},
url={https://openreview.net/forum?id=d0gMFgrYFB}
}